In my first article about the Structure of a Digital Image, I busted some of the myths and jargon which surround the pixels which go to make up digital images. This article goes on to describe how the computer quantizes the tones in an image. A third article will explain how color is analyzed. If you haven't already read the first article in this series, you may find it useful to do so before you read on.

Our long-established system of photographic imaging has a rich tonal range. The beautiful smooth transition in an image can be likened to a natural hill -- the valley floor denoting black, the summit white, with an infinite number of shades of gray in between.

HIKING

To represent gray, we can walk up the hill and stop when we sense that we are the same distance from the top as from the bottom. Half way up represents mid gray -- mid way between black and white.

Try it. Walk half way up a hill and put a mark down on the ground. Then go back to the bottom and walk up again until you sense that you are once more at the half way point. Now look down to see how close you are to your original mark. Is it in front of you, behind you -- or are you really lucky, discovering that it is right under your feet? That's hardly likely, for it's difficult to know precisely where you are on a slope. That's the way it is in our infinitely variable analog world.

Another analogy of analog is a household lighting dimmer switch. A small dial is turned to dim the lights from full-on to zero. These dials are rarely calibrated. Dimming the lights down "to half" entails a subjective assessment of what is half. Though this may be good enough for the mood of the room, it's not precise enough for digital imaging. Most importantly, it's not repeatable with accuracy.

STEP RIGHT UP!

A staircase is a kind of man-made hill. It's much easier to know when you are half way up a staircase, because you can count the steps. Take a short flight of seven steps and count them as you climb. One -- two --three -- four, stop. There are three steps below you, three steps above you. You are half way up, and also half way down. Half way represents mid gray. Could we be on to something useful here?

The difference between analogue and digital is rather like the difference between a slope and a staircase. Cut steps into a hillside and you can count the steps as you climb, giving you the ability to know precisely where you are in relationship to the top and bottom. Provide click-stop positions on a lighting dimmer and you can count the clicks. Sample an image, reducing it to a number of steps of gray, and you can define each tonal level precisely. But how many different tonal steps do you need to reproduce tone so that it looks continuous, so that the individual steps are so small that we don't notice them?

BASIC BITS

Computers are simple devices at heart. They just count, and the smallest pieces of data they can handle are called 'bits'. Just like a light switch, that bit can either be 'off' or 'on'. Unlike a domestic lighting dimmer, there is no state in between.

OR

Each bit may be assigned a value of '0' or '1' and we can use these two states to represent two tones -- say black and white -- for each of the pixels in our image. This equates to just one step -- not exactly a staircase.

This is the result of assigning just one computer bit to each pixel in our image. We can have either black or white, with no gray tones in between. Everything below mid gray becomes black, everything above mid gray becomes white. This is how computer displays looked before graphics came along.

If we use two computer bits to describe each pixel, they can either both be 'off', or the first one 'off' and the second 'on', or the first one 'on' and the second 'off', or both 'on'. This allows us four states -- black, dark gray, light gray and white. Are you keeping up? Here it is diagrammatically and pictorially.

Representing an image in only four tonal values can hardly be said to be 'photographic' in quality, though the extra two tones are a step in the right direction.

Adding a third bit increases the number of states to eight. These are all the various combinations.

 

A staircase of seven steps gives us eight clearly defined levels between ground (level zero) and upper floor (the seventh step and, therefore, the eighth level). If applied to every point on an image, would eight steps be enough to represent a continuous tone image? Let's see what describing an image in eight tonal steps gives us.

Seven steps give us eight levels, if we count the ground floor and top step. Ground represents black in our image, the top white, with six shades of gray in between.	With black, white and six tones of gray in between the image still looks posterized. Eight steps is not enough for full tonal representation.

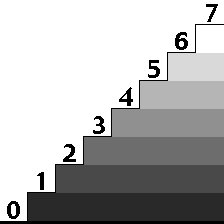
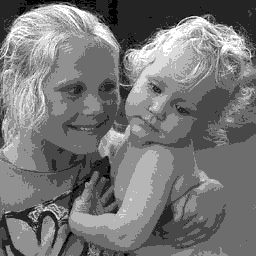
It's clear that we need more than three bits per pixel. The big question is -- how many bits per pixel do we need to display our image with full tonality on the computer screen?

CHARTING THE STEPS

I think you've got the light switch analogy by now. Showing banks of up to eight switches in all their two hundred and fifty six combinations of 'on' 'off' states would be too much for both of us. So I'm going to show you in chart form from now on.

This chart shows all the gray tonal values which computers can display, together with how many computer bits are required to describe them. Notice that we term the number of bits used to describe each pixel of an image as the "bit depth".

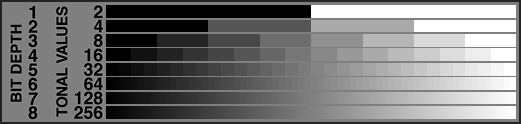
The top three tonal scales are the ones we worked through earlier. A bit depth of one gives us two tonal values, a bit depth of two gives us four tones, and a bit depth of three gives us eight tones.

Note that the number of tones doubles for each additional bit devoted to describing each pixel. By the time we get up to six bits per pixel (64 tones) it becomes difficult to differentiate between the individual progressive tonal steps. For seven and eight bits per pixel, the tones appear smooth and stepless.

You can't see the individual steps -- though they're there -- in this 8 bits per pixel (256 tone) image …	… unless you look very closely, as in this close-up section.

At 8 bits per pixel (256 tones) we have what appears to be stepless photographic quality.