THE STRUCTURE OF A DIGITAL IMAGE
Part One: THE DIGITAL ANALYSIS OF DETAIL
by John Henshall
The smallest element of a conventional photograph is a piece of grain. The equivalent smallest element of a digital picture is a pixel. The pix part of this word is from picture, the el from element. Join them together and you have pixel.
Digitising an image is like overlaying a wire mesh over a scene, analyzing the color and brightness seen through each hole in the mesh, then noting down the values in correct order in a huge list. How many of these pixels do you need to describe your image? Just like conventional photography, we don't want them to be large enough to be intrusive on our images, so the more the better - to a point. That point is when you simply can't see the extra detail that more pixels bring to the image. All the rest are wasted.
An important concept to grasp is that while both a digital camera sensor pixel and a monitor screen pixel do have physical sizes, an image pixel does not. A camera pixel is microscopic in size -- millions being crammed onto a sensor just a few millimetres across. Your monitor screen's pixel size is fixed forever when the screen is manufactured - just as its counterpart, the grain in silver halide photography is fixed in size when the film is manufactured. There may be 72 monitor pixels per inch, or perhaps up to 96 pixels per inch.
On the other hand, a digital image pixel has no physical size until you give it one. Until then, it is simply a mathematical definition inside the computer. It's up to you to decide how large to display that description. it's also important to note that each pixel is of uniform brightness and color across its whole area, irrespective of its size.

|

|

|
|
One image pixel is displayed here as one screen pixel (look closely!) This represents the maximum resolution (the smallest amount of detail) your monitor screen can display.
|
The same pixel displayed as ten screen pixels by ten screen pixels...
|
... and as forty screen pixels by forty screen pixels.
|
How many pixels you need in an image depends on the size and/or viewing distance of the finished image. In the accompanying series of color illustrations, I first (left) display all the pixels used to define the image - be there one or 65,536 of them - at the same size as the original scene. Then, to the right, the same image displayed at one image pixel to one screen pixel.
Click to continue
/basics/images/tg.gif)
|

|
Let's look at a typical scene: a blonde girl -- my daughter Martien -- wearing a magenta and blue T-shirt, holding a blonde baby boy -- her cousin Pieter. Behind the pair is dark green woodland and sandy ground.
Click on the image to continue
|
/basics/images/tg.gif)
A one pixel image -- filesize of 3 bytes required to store in computer
|

|

|
|
If we average the color and brightness of the scene, this is what we get -- a mixture of all the tones and colors in the scene
The smallest possible number of pixels we can use to describe an image is one. This is a one pixel image. Not exactly an exciting representation of the original scene, is it? But it does have a use.
What it tells the photographer is the average color and brightness of the whole image -- just like a reflectance exposure meter.
Click on the image to continue
|
This is the same single pixel displayed at 100% -- one image pixel as one monitor screen pixel.
|
/basics/images/tg.gif)
|

|
|
|
Now let's examine the image through a coarse wire mesh -- only 2 squares by 2 squares.
Click on the image to continue
|
|
/basics/images/tg.gif)
2 x 2 pixels (total 4 pixels) -- filesize 12 bytes
|

|

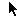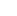
|
|
This is what we get if we average the color and brightness seen through each square of mesh, then remove the mesh overlay.
In the resulting four pixel image we can just begin to see some differences in colors in the four corners of the image but not much else. In fact the image is of less use than the one pixel image.
Click on the image to continue
|
The same image displayed at 100% -- two pixels wide by two pixels high on your monitor screen.
|
/basics/images/tg.gif)
|

|
|
|
Now let's make the mesh smaller -- 4 squares by 4 squares.
Doubling the number in each direction gives us 4 x 4 pixels -- a total of sixteen -- four times as many as before.
Click on the image to continue
|
|
/basics/images/tg.gif)
4 x 4 pixels (total 16 pixels) -- filesize 48 bytes
|

|

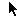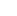
|
|
Let's average the color and brightness seen through each square of mesh and then remove the mesh overlay.
Doubling the resolution of an image isn't as simple as just having twice as many pixels. In fact doubling the resolution of an image requires four times as many pixels because we have to double the number in each direction. This is the square law in action.
Click on the image to continue
|
The same 4 x 4 pixel image displayed 4 pixels wide by 4 pixels high on your monitor screen.
|
/basics/images/tg.gif)
8 x 8 pixels (total 64 pixels) -- filesize 192 bytes
|
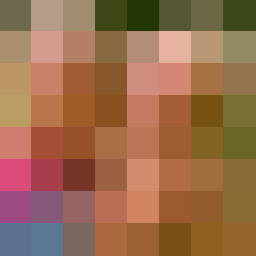
|
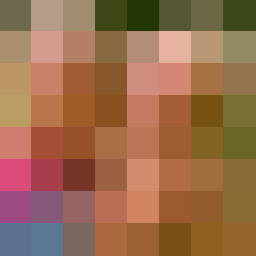
|
|
Doubling the number of pixels each time brings increasing higher resolution of the scene. Even as low as 8 x 8 -- a total of only 64 pixels -- Martien's blue and magenta T-shirt is just beginning to take shape.
Click on the image to continue
|
The same 8 x 8 pixel image displayed at 100% on your monitor screen. Can we just make out the two faces -- or is it my imagination?
|
/basics/images/tg.gif)
16 by 16 pixels (total 256 pixels) -- filesize 768 bytes
|
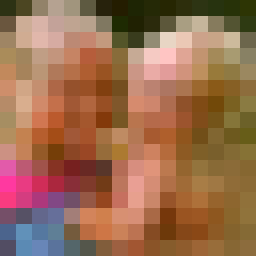
|
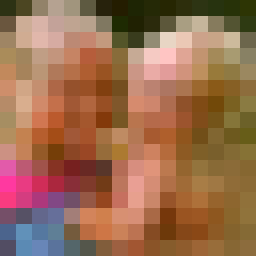
|
|
Note how the resolution improves as the number of pixels increases. And notice, too, how fast the total number of pixels in each successive image increases -- up from 64 pixels in the previous image to 256 pixels in this image. That's another effect of the square law.
Click on the image to continue
|
The same image displayed sixteen pixels wide by sixteen pixels high on your monitor screen -- at 100%. This is the largest size this 16 x 16 pixel image can be displayed without making the individual pixels obvious. Note that the subjects can now just be made out -- this time it's not my imagination.
|
/basics/images/tg.gif)
32 by 32 pixels (total 1,024 pixels) -- filesize 3,072 bytes
|

|

|
|
The number of pixels again quadruples -- this time from 256 to 1,024 -- and the filesize which would be needed to store this image uncompressed in the computer jumps from 768 to 3,072 bytes.
Now is the time to note that everything in a digital image -- even the gentle curves of a young face -- must be described by a series of squares.
Click on the image to continue
|
This is the same image displayed thirty two pixels wide by thirty two pixels high on your monitor screen. It looks clearer at small size, doesn't it?
|
/basics/images/tg.gif)
64 by 64 pixels (total 4,096 pixels) -- filesize 12,288 bytes
|

|

|
|
The jump from 1,024 to 4,096 pixels is the biggest yet. The resolution is much better but still the image looks blocky.
Click on the image to continue
|
This is the same image displayed 64 pixels wide by 64 pixels high on your monitor screen.
|
/basics/images/tg.gif)
128 by 128 pixels (total 16,384 pixels) -- filesize 49,152 bytes
|

|

|
|
Up from 4,096 to 16,384 pixels, at last the pixels are not too obtrusive and we can clearly recognize our subjects. But the image somehow seems to lack sharpness and the hair still looks blocky.
Click on the image to continue
|
The same image displayed 128 pixels wide by 128 pixels high on your monitor screen. No sign of pixels and our subjects are easily recognizable.
|
/basics/images/tg.gif)
256 by 256 pixels (total 65,536 pixels) -- filesize 196,608 bytes
|

|

|
|
At 256 x 256 -- a total of 65,536 pixels -- individual pixels have merged to become imperceptible at monitor screen resolution. The main improvement for the 49,152 increase in pixels needed to double the resolution from the previous example is better image sharpness.
|
The same image displayed 256 pixels wide by 256 pixels high on your monitor screen -- now identical in size to the picture on the left.
|
We could go on doubling the resolution of our image but, for the size of reproduction shown above, no improvement would be apparent. Such "unseen" resolution in the image would however mean that the image could be enlarged to a larger size, if required. This is similar to the size of print obtainable from a film negative. It is no more mysterious than that. How big can you enlarge a digital image? Just as with traditional photography, it all depends on what you feel is acceptable for the size of print (or other means of display) and viewing distance.
Of course, the image doesn't have to be square as in our examples. I've used a square image simply to make the explanation simpler.
At this point it is interesting to consider one of the major selling points of digital cameras: pixel count. In 1998, one-megapixel cameras were big news. We've since seen two-, three-, four-, five- six-, seven- and eight-magapixel cameras come along, to big fanfares. Pixel counts in professional DSLR cameras now go much higher -- up to 21 megapixels in the Canon 1Ds Mark III.
What's a megapixel or two among friends? People note that one camera has "only" 6 megapixels compared to, for example, another with 6.3 megapixels. In fact, the difference is minute.
To double the resolution of a one-megapixel camera, we have to go to four-megapixels -- not two-megapixels. To double the resolution of a three-megapixel camera we have to go to twelve megapixels. To double the resolution of a four-megapixel camera, we'd have to go to no less than sixteen-megapixels.
Why is this? Well you can't just double the number of pixels ACROSS the image -- you also have to double the number of pixels DOWN the image. This means that, to havec DOUBLE the resolution, you have to FOUR TIMES the number of pixels.
Displaying the image on a computer screen, or making a digital print, is just like coloring in the squares on a piece of graph paper. When you remember that the digital "graph paper" could have around six million tiny squares for just one image digitised from a piece of 35mm film, the process is quite phenomenal.
Now we can go on to analyse the TONE in an image.

All text and photographs are Copyright © 2005-2008 by John Henshall. All rights reserved.
|
![]()
![]()
![]()
![]()
![]()

